Merge sort 병합정렬

2016년 1학기 자료구조 수업시간에 배운 내용이 이번 알고리즘 수업 시간에서도 나와서 여기에 정리한다.

그림

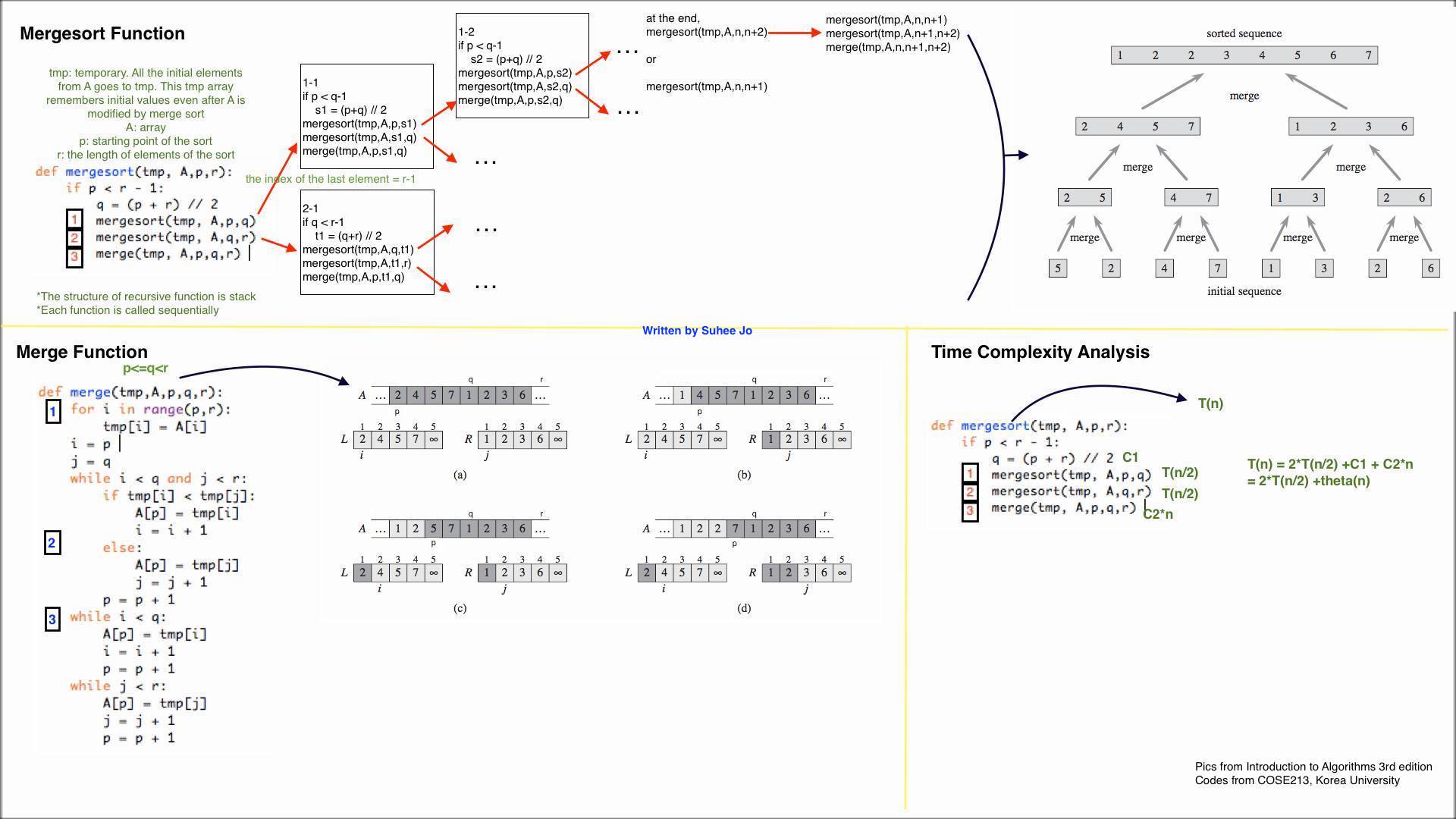
알고리즘 설명

병합정렬 merge sort 의 핵심 알고리즘은 이것이다 - Divide and Conquer. 한번에 해결할 수 없는 문제를 작은 단위로 쪼개서 해결한 다음 이어붙이는 것. 그런데 어떻게 쪼개고 이어붙일 것인가? 임의의 단위로 쪼개고 이어붙이면 알고리즘이 복잡해지고 비용도 많이 들 것이다 일정한 단위로 쪼개고 이어붙이는 행위를 반복할 수 있도록 하는 재귀함수 recursive function 을 만들면 이 문제를 해결할 수 있다.

병합정렬에서는 숫자들의 배열을 둘로 쪼개는 것을 반복한 뒤 divide , 가장 끝에 쪼개진 요소들끼리 대소비교 후 차례대로 배열에 집어넣는다. conquer

알고리즘 구현

대략의 작동원리를 알았으니 이제 그림으로 넘어가서 어떻게 실제로 코드로 구현되는지 살펴보겠다. merge sort는 함수로 구현되는데, 이 함수는 두 부분으로 이루어져있다. Divide 부분인 mergesort, Conquer 부분인 merge 이다. mergesort 는 주어진 array를 두 부분으로 쪼개는 것을 반복하며 merge는 쪼개진 두 부분을 합치게 된다. merge 에서 두 array를 합칠 땐 그냥 합치는 것이 아니고 각 element 간 대소비교를 해서 합친다. 각 함수의 parameter에 대한 설명은 그림에 적혀져있다.

mergesort

mergesort는 재귀함수 recursive function 이다. mergesort(tmp,A,p,r) 를 두 부분으로 쪼개서 (2등분, 홀수일 땐 짝/홀로 나눠짐) 다시 mergesort가 이루어진다. 끝에 가면 어떻게 될까? 결국 이런식으로 쪼개다 보면 마지막 node에는 mergesort(tmp,A,0,2) 혹은 mergesort(tmp,A,0,1) 이런 식으로 두 가지가 남는데 후자는 p<r-1를 만족하지 못하므로 실행이 안되고, 전자는 p<r-1을 만족시키니까 실행하면 mergesort(tmp,A,0,1) mergesort(tmp,A,1,2) 그리고 merge(tmp,A,0,1,2) 가 남는다. mergesort(tmp,A,0,1) mergesort(tmp,A,1,2) 모두 조건을 만족시키지 못해 실행이 불가능하다. merge함수만 실행가능한데 이 때 merge 함수가 하는 일은 더 이상 쪼갤 수 없는 A[0], A[1]을 대소비교해서 합쳐서 array에 넣는 것이다. 이 과정을 도식화한 것이 그림에 나와있다. mergesort란 merge 가 제 기능을 할 수 있도록 array의 요소들을 쪼개주는 기능을 하는 것이다.

merge

merge 함수의 목적은 array A에서 A[p:q-1]와 A[q:r] 두 array 의 element를 서로 비교해서 A에 sort 해서 넣는 것이다. 이를 실행하기 위해 다음과 같은 방법을 쓴다. 처음에 받은 A의 A[p:r]까지의 값들을 tmp 즉, temporary array에 저장해둔다. 그리고 처음에 받은 p와 q값을 각각 i,j에 저장한다. 이 i,j는 각각 A[p:q-1]와 A[q:r] 의 범위 안에서 움직이고, 서로의 값을 비교해서 작은값 먼저 A[p]에 집어넣는다. 한 차례 비교가 끝나면 p는 1만큼 오른쪽으로 이동한다.

Time Complexity Analysis

그림 참조