Heap sort 힙정렬

저번에 이어서 2016년 1학기 자료구조에 나온 내용과 알고리즘 수업의 내용이 겹쳐서 함께 정리한다. Merge sort 와 Heap sort 의 코드 모두 자료구조 수업에서 받은 것들이다.

그림

알고리즘 설명

Merge sort 가 Divide and Conquer 를 이용한 algorithm 이라면, Heap sort 는 Heap이란 Data Structure를 이용한 algorithm이다. 따라서, Heap sort를 하기 전에 Heap이란 자료구조에 대해서 알아볼 필요가 있다.

Heap 이란?

1. Graph 그래프는 V와 E의 ordered pair 이며, 이 때 V 는 vertices(nodes)의 집합이며, E는 edges, 즉 unordered pairs of vertices(ordered pairs 는 arcs라고 함)의 집합이다. Graph = ( V, E)

2. Tree Graph 중에서도 undirected, connected, acyclic 한 그래프를 Tree 라고 한다.

Tree의 node 중에서 가장 꼭대기에 있는 노드를 root라고 한다. 나머지 노드들은 서브트리로 분할될 수 있다. Root r에서 node y 로 가는 하나의 단순한 path 에서 x를 거쳐간다면 x는 y의 parent, y는 child 이다.

Binary Tree 즉 이진트리는 각 트리의 node가 child node를 최대 2개씩 가지고 있는 트리를 말한다.

Full Binary Tree는 맨 끝의 node를 제외한 모든 노드가 child node를 두 개씩 가지고 있는 트리를 말한다. Complete Binary Tree는 맨 끝, 그러니까 마지막 level을 제외하고 모든 노드가 2개씩 채워진 트리이며, 마지막 node는 왼쪽에서부터 채워진 형태이다. 위-> 아래, 왼 ->오 순서를 어기지 않고 child 노드가 채워진 형태. 왜 이런 타입을 따로 분리해놨는지 생각해보자면, Tree라는 추상적 자료구조를 컴퓨터 위에 구현하기 위해서는 숫자들인 array에 Tree 구조를 구현할 수 밖에 없기때문이겠지? 왼쪽에서부터 차있어야 array에서 구현했을 때도 각 인덱스에 tree의 어떤 node 가 들어가 있는지 예측하기 쉽기때문이다.

Heap은 Complete Binary Tree에 속한다. 여기에 Heap 만의 특성이 있는데, 바로 모든 Parent node가 Child node 보다 같거나 크다는 것이다. A(parent(i)) >= A(i)

알고리즘 구현

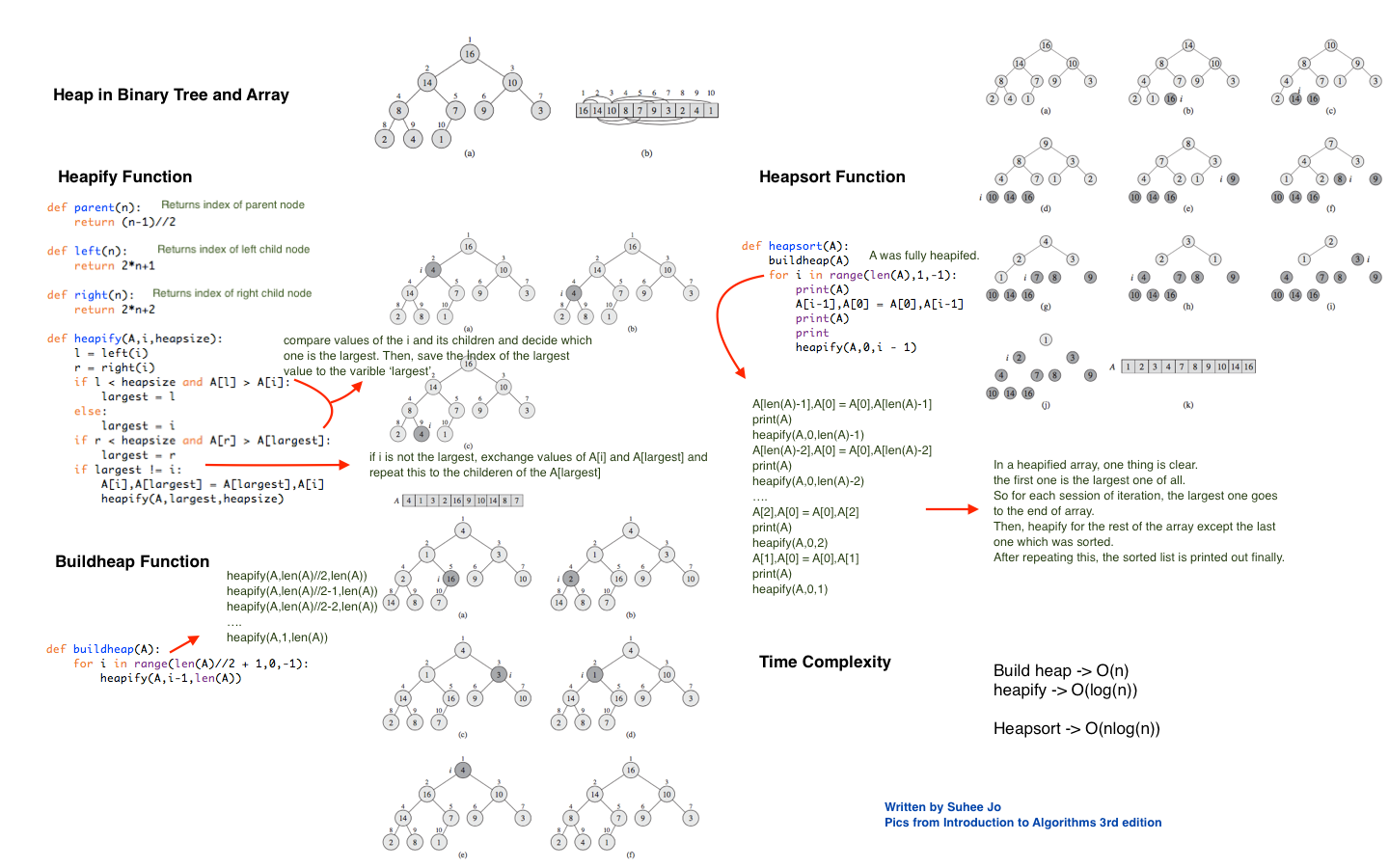
Heap sort 알고리즘은 3가지 function 으로 구현되어 있다. 첫번째는 heapify로 하나의 노드와 그 자식들 간의 대소비교를 통해 가장 큰 값을 가진 노드를

heapify

array A의 i 번째 인덱스의 노드와 그의 children을 비교해서 가장 큰 값을 가진 노드의 인덱스를 largest에 저장한뒤 만약 largest가 i 가 아니면, 즉 input으로 받은 i인덱스에 저장된 값이 자기 children보다 작으면, A[largest]를 i자리에, A[i]는 A[largest] 자리에 넣는다. 그리고 A[largest] 에 대해서 heapify를 반복한다.

buildheap

heapify(A, len(A)//2 , len(A))

heapify(A, len(A)//2 - 1 , len(A))

…

heapify(A, 1 , len(A))

왜 heapify를 len(A)//2 인덱스부터 시작할까? children이 없는 노드에 대해서는 heapify를 해줄 필요가 없다. 마지막 노드의 parent부터 root 까지만 heapify 를 해주면 된다. 이렇게 마지막 노드의 부모부터 위로 올라가면 heapify 가 빠짐없이 된다.

heapsort

힙을 build 했다면, 한 가지만은 확실하다. 맨 위의 노드, 즉 root 가 모든 element 중에서 가장 큰 값을 가진다는 것이다. 여기서 착각하면 안되는 것이, 2번째 노드가 3번째 노드보다 크다던지 하는 것은 보증되지 않는다는 것이다. 따라서 이런 성질을 사용해서 heapsort를 해보자. heapsort의 목적은 array A 를 수가 클수록 오른쪽에 오게 sort하는 것이다. 이는 다음과 같이 실행된다. 우선 array에서 가장 첫번째 요소, 즉 heapsort의 root 이며 가장 큰 수를 담고 있는 요소를 array의 가장 뒤로 보낸다. 대신 원래 가장 뒤에 있었던 요소는 root 자리에 오게된다. 이렇게 되면 원래 가장 처음 노드였던 것은 정렬되어 뒤로 가지만, 나머지 노드들을 보면 heap 이 완전히 깨진 상태이다. 이 때 heapsize 를 축소해서 마지막 노드를 제외한 노드들끼리 heap을 만든다. 이를 heapsize가 1이 될 때까지 반복하면 heapsort가 완성된다.

Time Complexity Analysis

heapify(A,i,heapsize)

i 번째 노드를 루트로 가지는 사이즈 n의 sub tree 에서, heapify의 러닝타임은 A[i]와 그 두 children에 대한 관계 조정하는데 theta(1)만큼 들고, i != largest 라서A[largest] 에 대해서 recurrence가 일어난다면 T(n) <= T(2n/3) + theta(1) 이다.