Kernel Fisher Discriminant Analysis
Kernel Fisher Discriminant Analysis
고려대학교 Business Analytics 강의 내용 중 Kernel Fisher Discriminant Analysis 에 대해 정리했습니다.
Linear Discriminant Analysis
Linear Discriminant Analysis, 즉 LDA는 projection 후 두 class를 가장 잘 분리하는 projection 축을 찾는 것입니다. Projection이란 말에서 알 수 있듯, LDA는 고차원의 데이터를 저차원의 데이터로 차원축소하는 것도 포함하고 있습니다.
데이터 공간 상의 한 점 x를 project한 뒤 다음과 같이 나타낼 수 있습니다.
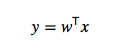
데이터 공간 상의 각 점들이 projection 평면 위에 표현되면 다음과 같이 나타납니다
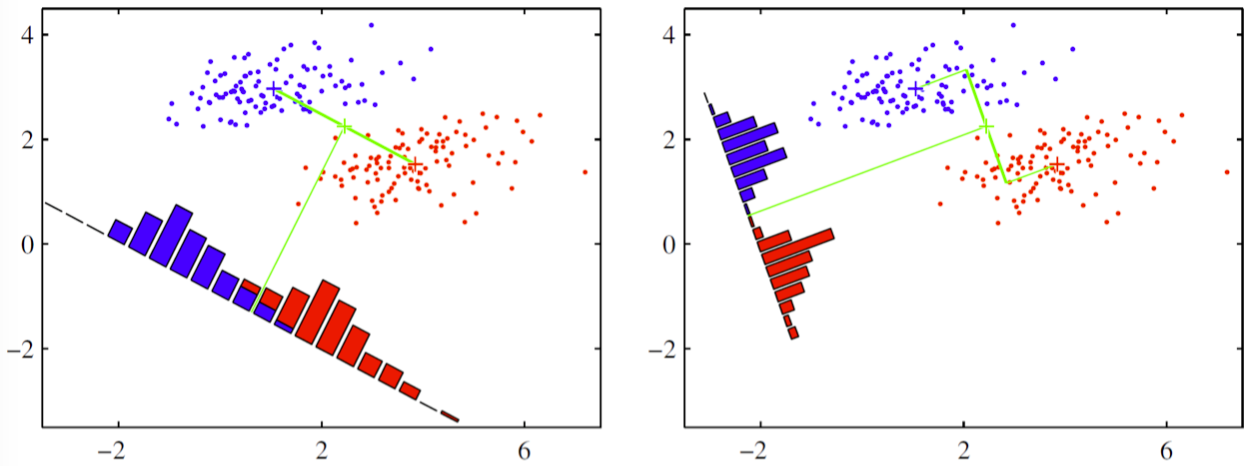
이 때, 우리의 목적은 분류를 해내는 것이므로 왼쪽과 같은 그림은 목적에 비추어 생각해보면 바람직하지 않습니다. Projection 후를 기준으로 삼아 분류를 해내기 위해서 두 가지 기준을 생각해볼 수 있습니다. “between class variance” 와 “within class variance” 가 그 두 가지입니다. 첫번째 between class variance는 두 class 가 얼마나 멀리 떨어져 있는지에 대한 지표입니다. 두번째 within class variance는 한 class의 샘플들이 서로 얼마나 가까이 밀집해있는지에 대한 지표입니다. between class variance가 커질수록 두 class는 멀리 떨어지게 될 것이고, within class variance가 작아질수록 한 class 에 속한 sample 들은 가까이 모이게 될 것입니다. 따라서 ‘분류’라는 목적을 생각해보면 between class variance를 크게 하고, within class variance를 작게 해야한다는 것을 알 수 있습니다. 이에 따라 우리의 목적함수를 나타내면 다음과 같습니다.
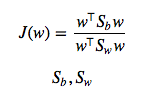
는 각각 between class, within class 의 covariance matrix 입니다.
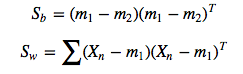
이 때 Lagrangian Dual과 KKT 조건을 활용 하면 다음과 같은 식을 얻을 수 있습니다.

즉 이것은 위에 대한 eigen value 문제이며, 가장 큰 eigenvalue에 대응하는 eigen vector w 가 우리가 구하고자 하는 것입니다.
아래코드는 위 수식을 통해 class 2 개의 데이터셋(아래 사진 추가함)에 대해 LDA로 w 값을 찾아낸 것입니다. 데이터셋은 랜덤으로 생성되기때문에 아래 사진은 예시입니다.
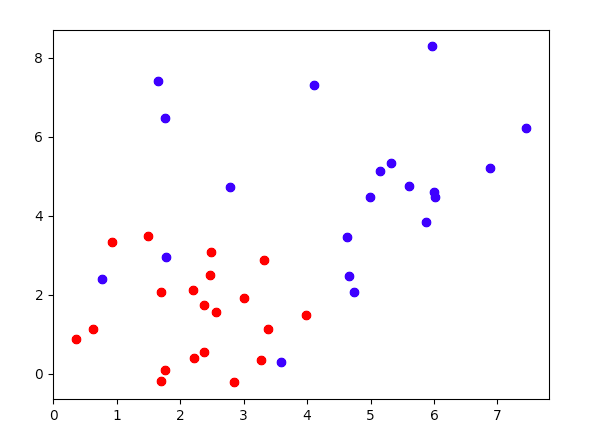
# 제대로 실행안되던 부분 수정했습니다
import numpy as np
import matplotlib.pyplot as plt
mu_x1, sigma_x1 = 2, 1
x1 = mu_x1 + sigma_x1 * np.random.randn(20)
mu_y1, sigma_y1 = 2, 1
y1 = mu_y1 + sigma_y1 * np.random.randn(20)
plt.plot(x1, y1, 'ro')
data1 = np.stack((x1, y1)) #shape (2,20)
mean1 = np.mean(data1, axis=-1)
mu_x2, sigma_x2 = 4, 2
x2 = mu_x2 + sigma_x2 * np.random.randn(20)
mu_y2, sigma_y2 = 4, 2
y2 = mu_y2 + sigma_y2 * np.random.randn(20)
plt.plot(x2, y2, 'bo')
data2 = np.stack((x2, y2))
mean2 = np.mean(data2, axis=-1)
all_mean = (mean1+mean2)/2
# between class covariance matrix
S_B = np.multiply(2, np.outer((mean1 - all_mean), (mean1 - all_mean))) + np.multiply(2, np.outer((mean2 - all_mean), (mean2 - all_mean)))
S_W = np.zeros(S_B.shape)
# within class covariance matrix
for i in range(20):
norm1=(data1[:,i] - mean1).reshape((2,1))
norm2=(data2[:, i] - mean2).reshape((2,1))
S_W = np.add(np.dot(norm1, norm1.T), S_W)
S_W = np.add(np.dot(norm2, norm2.T), S_W)
# objective function
mat = np.dot(np.linalg.pinv(S_W), S_B)
eigvals, eigvecs = np.linalg.eig(mat)
eiglist = [(eigvals[i], eigvecs[:, i]) for i in range(len(eigvals))]
eiglist = sorted(eiglist, key = lambda x : x[0], reverse = True)
# find w
w = np.array([eiglist[i][1] for i in range(2)])
Kernel Fisher Discriminant
앞에서는 Linear Discriminant에 대해서만 다루었다면, 이번에는 Kernel을 이용해 보다 복잡한 모델링을 시도해 보겠습니다. LDA에 커널을 적용한다면 어떻게 될까요?
우선 데이터셋 Z에 대한 full covariance 는 다음과 같습니다.
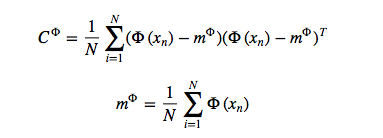
within class variance와 between class variance 는 다음과 같이 나타나게 됩니다.
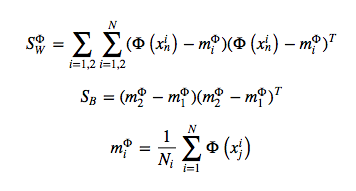
projected vector는 다음과 같이 나타나게 됩니다.
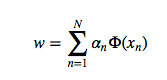
식을 풀어헤치면 결국 Objective function은 다음과 같이 나타납니다.
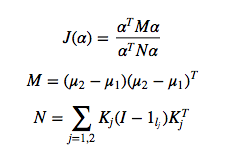
우리가 구하려는 것은

이고, kernel 에 의해 새롭게 주어진 데이터포인트는 다음과 같습니다.
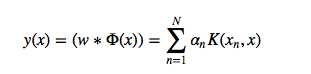
References </br> http://mlpy.sourceforge.net/docs/3.5/ http://goelhardik.github.io/2016/10/04/fishers-lda/
